Optimization algorithms to fit a structural time series model. The stsm R package

javi | May 26, 2025, 9:41 p.m.

The package stsm provides some utilities to fit the basic structural time series model.

As discussed here, there are several packages in R to work with the Kalman filter. Most of the packages mentioned there provide sound implementations of the Kalman filter as well as flexible interfaces to cast a broad range of time series models in state-space form. However, in my view, little attention is given to the procedure that optimizes the likelihood function. A general purpose algorithm --the L-BFGS-B algorithm-- is typically used. The stsm package provides specific algorithms to fit the basic structural time series model. Details are given in the the document provided with the package. For a quick example you can also see this post.

Here, I want to show a summary of some simulations where the convergence of a general purpose algorithm is compared to the Newton-Raphson and the scoring algorithms available in the package. These last two algorithms use the analytical expressions of the Hessian and the information matrix.

The plots below summarize the convergence observed in some simulations for the optimization of the frequency domain likelihood function, respectively for the local-level level model and the local-level plus seasonal component time series models. The scripts that replicate these and other simulation exercises are provided with the package.

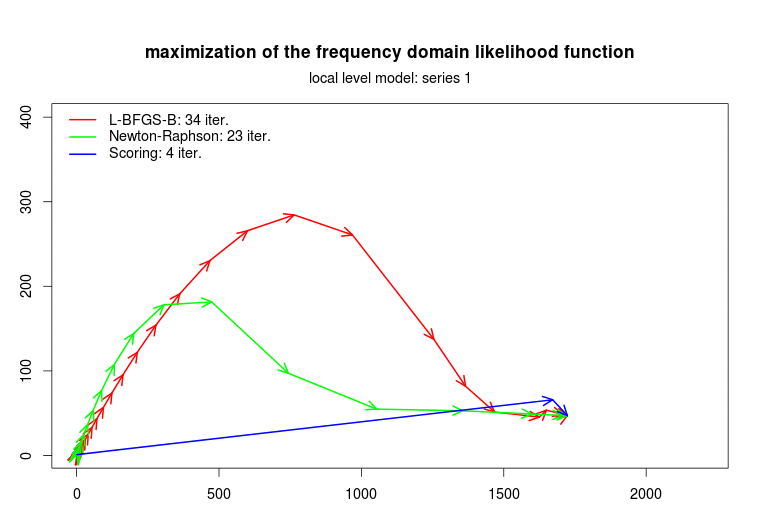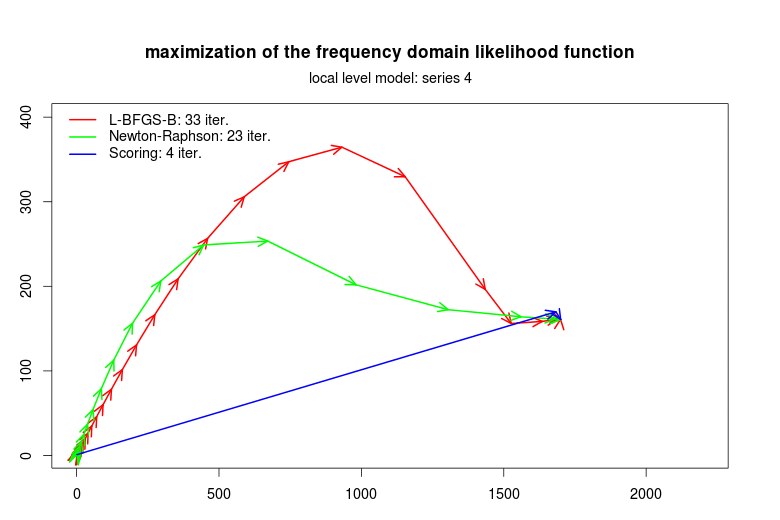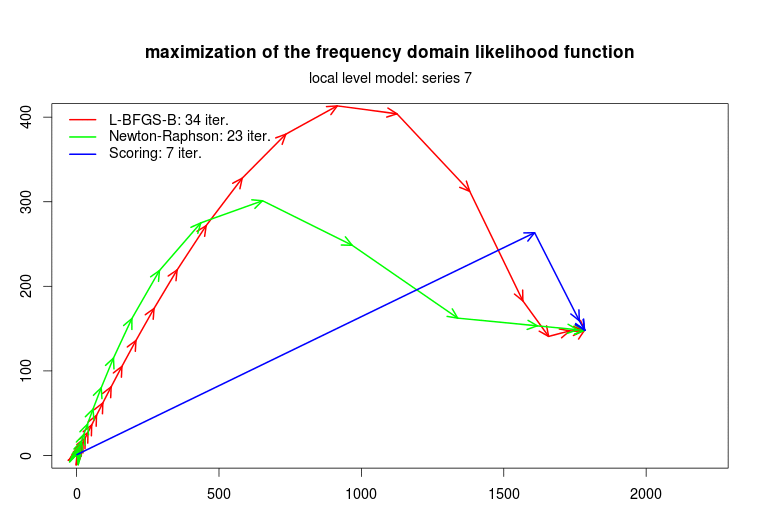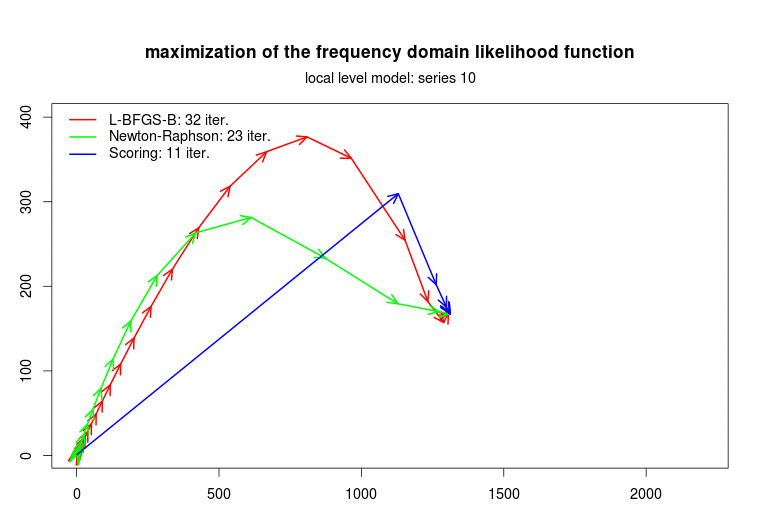
The Newton-Raphson algorithm (which uses the analysical Hessian) and the scoring algorithm (based on the information matrix) converge in fewer iterations that the L-BFGS-B algorithm. The advantage of the L-BFGS-B algorithm is that no matrix inversion is required because the inverse of the Hessian is numerically approximated. These results suggest that the performance of general purpose optimization algorithms can be improved by specific algorithms as those implemented in stsm.